「数の計算からあらゆるものの計算へ」コンピュータの基礎・チューリングマシンとはなにか？

どうも、木村（@kimu3_slime）です。

スマホ・パソコン・インターネットは、ここ100年の世界を大きく変えてきました。このブログも、その恩恵によって作られたものと言えます。

さてそれが形になっているのは、コンピュータというものを誰かが生み出したからです。

今回は、コンピュータの父と呼ばれるアラン・チューリングと、コンピュータの基礎となった考え方であるチューリングマシンを紹介したいと思います。

チューリングとは

画像引用：AlanTuring.net

アラン・チューリングは1912年、イギリスに生まれました。数学や科学全般が小さい頃から得意で、のちに数学者、論理学者、暗号解読者、コンピュータ科学者として知られるようになります。

彼の半生を扱った映画「イミテーション・ゲーム」はオススメ。

第二次世界大戦のときにドイツが使っていた暗号生成装置「エニグマ」を、チューリングが解読としていくというもの。

また、最近では人工知能の話題をニュースで目にすることも増えましたが、機械が知能を持っているかどうか判別するテスト（チューリング・テスト）を作った業績も有名ですね。

チューリング・マシンとはなにか

さて、エニグマの話とチューリング・テストの話は、一般向けにわかりやすく紹介されていますが、肝心のチューリング・マシンの話はまだまだ分かりにくいものが多い印象です。

だからこそ、できるだけわかりやすく紹介したいと思います。

チューリング・マシンは、1936年の論文「計算可能数とその決定問題への応用（On computable numbers, with an application to the entscheidungsproblem）」で提唱された仮想の機械。万能計算機械（universal computing machine）とも呼ばれます。

コンピュータは、日本語に直せば計算機ですが、単なる計算機は電卓と呼ばれます。

コンピュータというときには、あらゆる計算・プログラムを実行できる機械のことを指しているのです。つまり、万能マシンのことを指しています。

どうやってそのあらゆるものを「計算」するのか、それがチューリング・マシン（万能マシン）のアイデアなんですね。

チューリング・マシン誕生の背景

そもそも、なぜチューリングはあらゆるものを計算しようとする機械（万能マシン）を考え出したのでしょうか。

その背景には、数学者ヒルベルトが出した問題「ヒルベルト・プログラム（決定問題）」があります。

ヒルベルトは現代数学の父とも呼ばれる数学者で、「ヒルベルトの23の問題」など多くの未解決問題を提唱しています。

ヒルベルト・プログラムは、簡単に言えば、数学を完璧にしようとするものでした。

数学というのは、問題（命題）の真偽を証明することの連続です。「命題：√2は無理数である。証明：なぜならば〜」という矛盾ない証明があるからこそ、誰にでも理解できる数学ができあがるというものです。

ヒルベルト・プログラムは、「真である命題は（有限回の手続きで）必ず証明できる」「公理（推論の基礎となる仮定）からどれだけ推論をしても、矛盾が示されることは決してない」かどうか、完全性と無矛盾性を問うものでした。

この問題に挑戦して結果を残したのが、不完全性定理を示したゲーデルと、チューリングマシンを生み出したチューリングです。ヒルベルトがやろうとしていたことは不可能だよ、と言ったのです。

「チューリング情報時代のパイオニア」から引用しましょう。

ヒルベルトは数学には真か偽かを決める崇高な唯一の系統的手順があるはずだと考えていた。ニューマンが錬金術師が鉛を金に変えた伝説的な話にひっかけて皮肉を込めて読んだように、この「新しい賢者の石」があれば、ある数学的な記述が真か偽かを誰もが洞察や直観や創造性なしにはっきりとさせることができる。ヒルベルトは、こうした崇高な系統的手順の存在が、数学全体を「誰もが同意できる強固な基盤の上に」築くために必要だと言明した。

ゲーデルの成果はこの崇高な系統的手順の存在に対する信念を揺るがすもので、ついにはチューリングがそんなものは存在しないとする説得力のある論議を生み出したのだ。もしそんなものが存在するなら、系統的手順は何でも実行できる万能チューリング・マシンがそれを実行できる。そして新しい賢者の石としての万能チューリング・マシンは、すべてのイエスとノーで答える問題を解くことができる。しかしチューリングは、万能チューリング・マシンは、イエスとノーで答えられる数学の問題をすべて解くことはできないということを、一点の曇りもなく証明してしまった。このことから必然的に、ヒルベルトの市場の系統的手順は存在できなくなる。

引用：チューリング情報時代のパイオニア

チューリング・マシンは、数学の形式体系・プログラム（問題）をすべて落とし込んで実行できる機械です。しかし、そんな機械でも解けない問題がある（停止性問題）ということをチューリングは示しました。つまり、数学には解けない問題があるということを示してしまったのです。

「数学の基礎・証明をきちんとしたものにしよう」というヒルベルトの発想があって、その結果チューリング・マシンが生まれてきた、という流れですね。

もともとは純粋に数学的な問題でしたが、やがてコンピュータを生み出し社会を変えることになった良い例と言えるでしょう。

チューリング・マシンとは

チューリング・マシンの概要については、十分に述べたかと思います。

果たしてそれはどう構成されているのか、簡単に紹介します。

それは、（仮想の）テープとスキャナーの2つからできています。

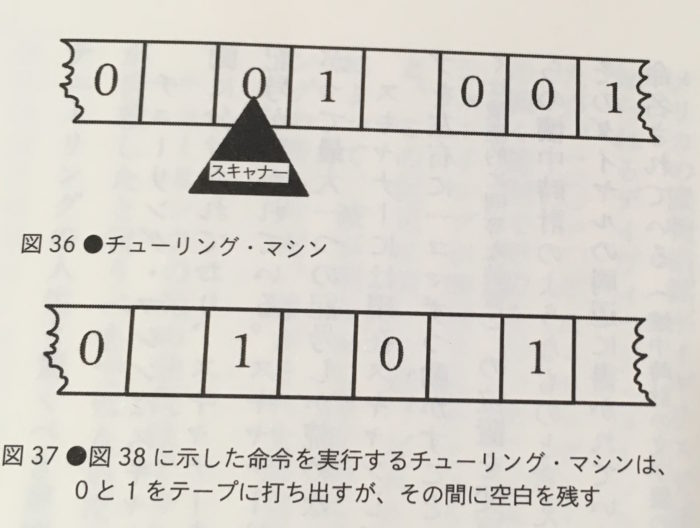
画像引用：チューリング情報時代のパイオニア

テープは、区画に分かれていて、そのひとつにひとつの文字を保存しておくことができます。

スキャナーは、常にテープ上の1区画に位置して、その区画の状態を読み書きできます。区画にある文字を消去したり、印字したり、左右に動くことができるものです。

現代の言葉で言えば、テープはHDD・メモリなどの記憶装置、スキャナーはCPUなどの処理装置に対応していると言えるでしょう。

ここでテープ・スキャナーに加え、それらがどう動くかという命令表を加えます。これはプログラム・OSに対応するものですね。

命令表とは、テープに書かれた情報とスキャナーの動作を対応させるものです。

例えば、「010101……」という文字列を出力する命令表は、次のようになっています。「最初はすべて空白のテープから始めるとする。状態1.スキャンしている区画が空白なら、0を印字してスキャナーを右に動かす。状態2に進む。状態2.スキャンしている区画が空白なら、1を印字してスキャナーを右に動かす。状態1に進む。」

めちゃくちゃ簡単なプログラムですが、ポイントはあらゆる問題を入力・実行できることです。

概念としてテープは無限の長さを持っていて、プログラム（命令表）さえ作れば何でも計算できてしまうのです。

例えば、円周率のように無限に桁を持っている数値も、チューリングマシンなら計算することができます。無限に桁は続くけれども、計算式は有限の情報で書けるので、数値を示し続けることができるわけです（これは計算可能数と呼ばれます）。一方で、計算不可能な数も存在することをチューリングは示しました。

テープ、スキャナー、命令表（現在の言葉で言えば、メモリ、CPU、プログラム）のセット。これがチューリングマシンです。

これさえあればなんでも計算させることができる。実際には、無限のテープを用意することは不可能なわけですが、それでも概念の上であらゆる問題を設定し実行できる装置を思いついた、という点は素晴らしいですね。

チューリングマシンは単に数を計算する計算機ではなく、文字に落とせる論理式も計算できる万能計算機です。もはやコンピュータと言ってもいいと思います。

続いては、チューリングの発想をより具体的に、現代に残るような形（ノイマン型コンピュータ）にしたノイマンの話をしてみようかなと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。