「数学・自然科学」の記事一覧

「数の計算からあらゆるものの計算へ」コンピュータの基礎・チューリングマシンとはなにか?
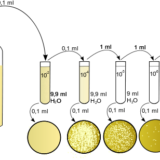
微生物はいかにして人間に知られたか 服部「微生物を探る」を読む
![]()
「ミーム」の起源・ドーキンス「利己的な遺伝子」を読む
![]()
Twitterで話題のハッシュタグ「 #数学和歌を詠もう 」とは?

「数学する人生」数学者・岡潔が詠った日本の情緒

数学を専門的に学んでいなくても面白い数学エッセー「数学する身体」

「女子高生アイドルは、なぜ東大生に知力で勝てたのか?」の「グルグル思考」に興味を持った理由

入門書「寝ながら学べる構造主義」を読む前に、僕と構造主義の出会いの話をする

戦争に飲み込まれた科学者の好奇心 マンハッタン計画と原子爆弾

何のために微分や積分を学ぶのか? 天体の運動とニュートンの運動方程式

なぜ関数という概念が生まれるのか? 自然の内在観
なぜ西洋において論理が重視され、日本ではそうではないのか? 近代合理主義と仏教の違い

数学を志す人のための本「志学数学」に教えてもらった、本をじっくり考えながら読む楽しさ

科学コミュニケーション論における欠如モデル、文脈モデルとは?

「いじめ」が記憶に残るのはなぜ? 記憶と情動の脳科学